How Small the World

In the late 1960s, Stanley Milgram conducted one of the most famous — and perhaps one of the most misinterpreted — experiments in the social sciences. He enlisted volunteers from far off lands (Kansas and Nebraska, in his case) to route a package to one of two target individuals in Massachusetts: a stockbroker in Boston, and the wife of a divinity school student in Cambridge. The catch was that participants could only forward the package to individuals that they personally knew (i.e., those with whom they were on a first-name basis), with the hope that this chain of personal contacts would eventually connect the source with the intended destination. Milgram’s stated aim was to study social interconnectedness, to establish whether two essentially random individuals inhabiting vastly different social spheres were in fact connected by short chains of intermediaries, or whether they existed in isolated communities separated by unbridgeable gaps. His elegantly designed experiment provided surprising support for the former hypothesis: Among the 44 chains that successfully made the trip from Nebraska to the Boston stockbroker, the journey was on average six steps long, a counterintuitively short stretch and one that suggests a certain social egalitarianism.
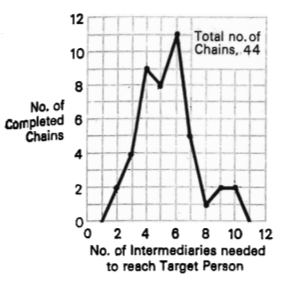
The view that six steps is “small” is the first persistent misconception, despite Milgram’s efforts to overthrow it. As Milgram points out, the completed chains are the “end product of a radical screening procedure” that filters out not only the hundreds of people any given individual is acquainted with, but that also excludes the friends of those unchosen individuals, and their friends of friends, and so on. Such exponentially growing sums are famously counterintuitive, as illustrated by the fable of the rice and the chessboard. If a chessboard were to have rice placed upon each square such that one grain were placed on the first square, two on the second, four on the third, and so on (doubling the number of grains on each subsequent square), how many grains of rice would be on the chessboard at the finish? A heap of rice larger than Mount Everest. The “small” six degrees that separate two random individuals, or the often only three steps separating one from the President, may shed light on how quickly a contagion can spread through a population, but it does not reflect the substantial social and psychological distance between them.
“A subtle misinterpretation of the small world phenomenon is conflating the statement that short paths exist between individuals, with Milgram’s more provocative suggestion that people can effectively navigate these paths.”
The second, and perhaps more subtle, misinterpretation of the small world phenomenon is conflating the statement that short paths exist between individuals, with Milgram’s more provocative suggestion that people can effectively navigate these paths. In the age of ubiquitous network data, describing whom we email, IM, or are connected to on Facebook, it has become possible to definitively assess the so-called topological question, with multiple studies confirming that typical individuals are in fact connected by paths of around six steps. In Milgram’s original experiment, the majority of started chains never reached their target, leaving open the possibility that those individuals who successfully completed the challenge were precisely those connected to the target by short paths, while those who didn’t were topologically distant. While I think it’s likely these chains died due to uninterested participants rather than a more fundamental roadblock, rigorously establishing the navigability of these paths has proven difficult. In a clever online replication of Milgram’s small-world experiment by Peter Dodds, Roby Muhamad, and Duncan Watts, tens of thousands of participants attempted to locate more than a dozen targets around the world. While the completed chains again exhibited short path lengths, attrition — and thus the potential selection bias problem — was even worse, with only a tiny fraction of started chains reaching their destinations.
In a new project, Lars Backstrom and Cameron Marlow at Facebook, and Duncan Watts and myself at Yahoo are again replicating Milgram’s experiment, this time on top of Facebook’s network of over 750 million people. By comparing the paths that participants ultimately select with their topological distances to the targets, we aim to mitigate the tricky selection bias problem. Hopefully, we’ll learn not only whether the world is small, but how well we can navigate our way around it.
To participate in our small world experiment, please visit sixdeg.net.
Bonus Puzzle
Say a pair of siblings each get married — to two people who are also siblings. Now if both couples have kids (if it sounds like anything incestuous is going on, reread the previous sentence!) lets call those kids übercousins. So we have a simple genetics question this time: How related are übercousins? (Here’s a geneticist failing to come up with the answer; let’s see how Messy Matters readers do…)
Illustration by Kelly Savage
