Ode to Power Laws
Anyone who knows me knows that I love power laws. What other distribution even comes close? The normal? Boring. Poisson? Too fishy. Hypergeometric? Ok, that one’s pretty cool, too. But still, power laws reign supreme in my mind.
Evidence of the mystical power of power laws is found by simply looking at references to “power laws” themselves. Parsing the 600,000 papers on the ArXiv,[1] one finds that the number of “power law” mentions in an article follows a power law! (Kudos to Aaron Clauset, Cosma Shalizi, and Mark Newman for the record-breaking 310 mentions of “power law” in their paper, “Power-Law Distributions in Empirical Data.”[2])
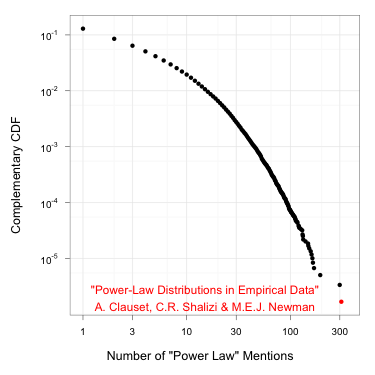
Now, some of the power law haters might look skeptically at the graph above, crankily insisting that proper statistical tests be applied before brazenly asserting the data follow a power law. To them I say, pshaw! I think with my gut. Others might say, so what?! — Do you call your BFF every time you see a normal distribution? There are so many ways in which power laws might arise, they argue, what have you learned by simply identifying one? My response: What would you learn if you found a lost Beatles track? Nothing — but it would be beautiful. Science is Truthiness, and Truthiness is Beauty.
As prose alone cannot adequately convey my fondness for power laws, I’ve written a haiku:
scale invariance
a universality
laws full of power
To ensure that the search for power laws continues, I propose that April 1st be national power law day. Go forth, and find yourself a power law!
Bonus Puzzle
30 ordinary dice (see below) are placed in a pitch dark room with the sum of the upward faces totaling 70. How can you divide the dice into two piles such that the sums are the same in each pile?
From Mathworld: “The most common type of die is a six-sided cube with the numbers 1-6 placed on the faces. For the six-sided die, opposite faces are arranged to always sum to seven. This gives two possible mirror image arrangements in which the numbers 1, 2, and 3 may be arranged in a clockwise or counterclockwise order about a corner. Commercial dice may, in fact, have either orientation.”
In other puzzle news, Dan Reeves is the new puzzle editor for SIGecom Exchanges. So if you want something more hardcore, check out his new puzzle in the current issue: Baffling Raffling.
Addendum
Congrats to Lev Reyzin, who solved what I thought was a pretty challenging brainteaser in a mere 30 minutes! (See his solution below.) The puzzle is our non-googleable version of one of my favorites: You’re in a pitch dark room with 20 coins, exactly 10 of which are heads up. How can you divide the coins into two piles having equal numbers of heads? This is really a great problem, so if you haven’t yet solved the dice version, give this one a shot (it’s a bit easier). Good luck!
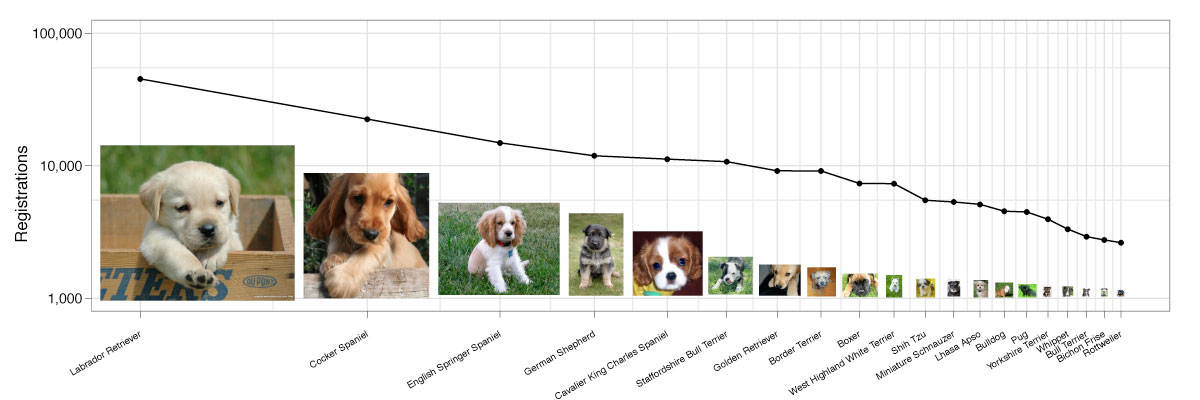
And now for some more power law antics. Duncan Watts asked, “Isn’t there some way to combine power laws and puppies? That would be even awesomer.” Well, I couldn’t agree more! So here’s some puppy power law data porn. And, yes, those registration statistics are real—puppy registrations do indeed follow a power law!
Footnotes
[1] Papers on the ArXiv are available for bulk download from Amazon S3.
[2] Counts are for case insensitive match of /power[- ]?law/ anywhere in any LaTeX document on the ArXiv.
Illustration by Kelly Savage