Stochastic, Nerdtastic Restaurant Bill Splitting

We have worked out what we believe is the fastest fair way to split a restaurant bill! You know what the state of the art is like so this is quite a breakthrough. To be clear about the “fastest fair way” it helps to compare to the extremes. First, the slowest fair way to split a bill is to compute exactly what everyone ordered. Groan. Dividing the bill equally avoids the hassle of figuring out who got what but is still pretty annoying, making change and whatnot. And of course that’s unfair to the people who ordered less, not to mention that it distorts what people order.
If you’re not a stickler for fairness and social efficiency, the hands-down fastest solution is credit card roulette: put everyone’s credit card in a hat and pick one. That person pays the whole bill. If everyone happened to have spent the same amount, then credit card roulette is also perfectly fair. [1]
The question, then, is how to get as close as possible to the convenience of credit card roulette but with perfect fairness: everyone pays, in expectation, exactly what they owe. Fortunately, and perhaps surprisingly, we don’t need to figure out who ordered what — for the most part — in order to achieve this.
Here’s what you do! Start with any item on the bill. The person who ordered that item pays the bill with probability equal to the cost of that item divided by the subtotal. Flip the appropriately biased coin [2]; if that person is it, then you’re done. If not, then subtract that item from the subtotal and repeat, recursively, with another arbitrary item. If you start with expensive items then you’ll probably find the person who’s paying after a handful of items, but it doesn’t matter for fairness what order you pick things in. You won’t have to figure out all the confusing drinks and appetizers (yet the outcome is as fair as if you had!).
Expectorant
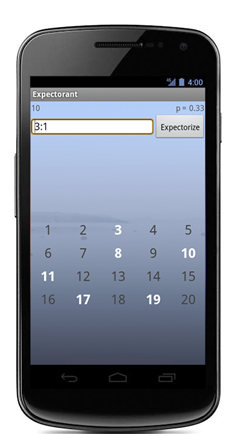
David Pennock is the one who first thought of this algorithm. We’ll leave it as an exercise for the reader to prove that it works. Proving that it’s the fastest fair algorithm should also be straightforward, once you pin down what “fastest” means. But enough theory. Bethany Soule and I wrote a little Android app [UPDATE: Now a web app] that makes this algorithm quite convenient. We call it Expectorant (“exquisite fairness in expectation”). Here’s an example of how it implements the above procedure:
Say the subtotal is $100 and the items on the bill are $5, $25, $60, and $10. Enter 100:5 and have the person who ordered the $5 item pick a number from 1 to 20. If their number is lit up (a 5% chance) they get to pay the whole bill! If not, amend the expression as 100:5,25 and repeat for the person who got the $25 item. They’ll “win” with probability 25/(100-5). If they’re off the hook, amend again to 100:5,25,60. This time most likely — p = 60/(100-5-25) — the $60 person will win the honor of paying the bill. If not, notice that 100:5,25,60,10 yields 10/(100-5-25-60) = 1. So if the process makes it to the last item on the bill then whoever got that item is it. Mathemagically, it doesn’t matter what order you put the items in — each person “wins” (pays the whole bill) with probability equal to their own fair share of the bill. In other words, you pay in expectation exactly your fair share. Including tax and tip, even though we never entered those. Pretty slick! Speaking of tips, remember you can minimize the hassle by starting with the most expensive items. Then you don’t have to figure out who most of the items belong to. Oh, and if 3 people split the $10 pickled monkey balls just treat it as 3 items, $10/3 each (expressions instead of numbers are allowed).
I bet I can game this by…
You really can’t! It doesn’t matter if you get two cheap appetizers instead of one entree or if you arrange to go first or last. Your probability of paying will be the sum of the costs of your dishes divided by the subtotal. That’s true even if none of your dishes were ever identified on the bill as yours. Another common question about this algorithm is what happens if no one gets chosen. The answer is that that can’t happen. If the process makes it to the last item on the bill then whoever got that item is it. But it rarely gets to the last item, which is the beauty of it. On average you’ll only traverse half the bill — and that’s half in terms of dollar value, not number of items. Which is much less than half the items if most of the bill is concentrated in a few expensive entrees.
To help see that the order doesn’t matter, that being up first is no better or worse than being up last, here’s a dirt simple example: Suppose three of us each ordered $1 items. The first person will pay with probability 1/3, just as they should. The second person pays with probability 1/2 if the first person is off the hook, which happens with probability 2/3. So the second person’s probability is 2/3⋅1/2 = 1/3. Perfect. And the third person will definitely pay if the first two people are off the hook, which happens with probability 2/3⋅1/2 = 1/3.
In general, the key to why this works, fairly, even without computing what everyone ordered, is this: Imagine a pie chart where everyone has slices of a unit pie in proportion to the amounts they owe. The total probability that you should pay is equal to the total area of your slices. But we can decompose that starting with one slice of size x, where your other slices total y. The probability you should pay is x + y which is x + y(1-x)/(1-x). That second term is what you get by renormalizing the rest of the pie after subtracting x. In other words, you first pay with probability x and then the rest of your probability (and everyone else’s) is covered in the recursive step, if you get to it.
Bonus Expectorizing
Expectorant is actually a more general tool. You can enter a probability (between 0 and 1) or an arithmetic expression that evaluates to a probability. A subset of the numbers 1-20 will light up such that any given number will be lit up with the given probability.
Here’s another way that’s useful. Say you owe me $7 for lunch but only have a twenty. If you give me the twenty with probability 7/20 then in expectation you’ve paid me $7! So type in 7/20 and tell me to pick a number from 1 to 20. Hit “Expectorize” — or have me do it so I know you didn’t cheat — and if my number is lit up then I lucked out and get the $20. (If you trust Expectorant to randomize properly — you can, we promise — then you can just always choose 1, or any number. [3])
We’ve even added some handy syntactic sugar to generalize the case of needing to pay someone with one of two amounts, one of which is too small and one which is too big. Entering something like 7@5,20 is a shortcut for (7-5)/(20-5). That’s the probability p such that (1-p)⋅5 + p⋅20 = 7. WTF? Here’s TF: If you have a five and a twenty and owe me $7, then give me the twenty with that probability and the five otherwise. Exquisitely fair (in expectation)!
Addendum: A Faster Fair Method!
There’s been a lively discussion of Expectorant on Hacker News since this went to press. The best comment was by Michael Donaghy who pointed out a faster version of the mechanism: Pick a uniform random number between 0 and the subtotal and walk down the bill adding up the costs (oblivious to who ordered what) until you hit the item that pushes you over the chosen number. Whoever ordered that item pays. One complication: if that item is something that occurs more than once on the bill then you need a way to disambiguate. You could randomize again or you could use a pre-decided ordering of the diners. Either way, you have to make sure to identify all the people who ordered that item. That’s perhaps a disadvantage compared to our version of Expectorant where items are always considered one at a time in isolation. But other than that, this version is certainly faster, and just as fair.
Related reading
- “You Do the Math” in the New York Times
- Academic paper that concludes that splitting evenly is inefficient
- Interview with the author of the above paper
- Splitting the bill at restaurants using game theory
- Advice columnists weigh in: “But I Only Drank Water”, “Dining out, I eat veggie … but pay like I ordered steak”, “A Measure of Guidance”, “But I Only Got the Soup”
- UPDATE: “Five Math Experts Split the Check”
Footnotes
[1] A common complaint about stochastic schemes is that they’re “only fair if you do it repeatedly with the same group of people”. That’s true if you insist on ex post fairness. We’re usually happy with ex ante fairness. Consider selling me a (perfectly fairly priced) lottery ticket for a dollar. That’s guaranteed to be unfair, ex post. Either you sold me a worthless piece of paper for a dollar, or I got a million dollars and only paid a dollar for it. But the fact that none of us knew which would happen made the one dollar price fair. Same story with venture capital investment, for example. You may need a gambling mentality to be down with it, but it’s quite fair even if only done once. The fact that it averages out in the long term to be perfectly fair ex post is icing on the cake.
[2] Here’s a way two people can flip a biased coin using nothing but their brains. It’s even quite robust to the notorious inability of humans to generate plausible random numbers. Person one writes down a fraction p of the numbers from 1 to 20. Person two guesses a number from 1 to 20. If their guess was one of the written down numbers, call the biased coin flip heads. We haven’t tested this rigorously but our sense from doing this a lot amongst ourselves is that the two people’s lack of randomness pretty much cancels out, particularly if they’re trying for opposite outcomes, and yields reasonably random Bernoulli outcomes. Of course with numbers 1 to 20 you’re limited to a granularity of 5% on the probabilities. You could use, say, 1 to 100 but that’s a bit unwieldy.
[3] There’s a very small way in which you do have to trust Expectorant: If the probability percentage is not a multiple of 5. For example, to get a 1% probability you’d need to light up a fifth of one of the numbers (1-20). That’s not allowed so Expectorant lights up one number with 1/5 probability. It always does this fairly for probabilities that don’t work out to an integer number of numbers lit up. In theory it could cheat and round in the wrong direction. But it doesn’t, so you’re actually getting probabilities to many decimal places of fairness, despite the discrete grid.
Illustration: Kelly Savage
The ingenious restaurant bill splitting algorithm was devised by Dave Pennock of, appropriately, oddhead.com.
Thanks to Sharad Goel and Kelly Savage for expectorizing the bill with us every time we go out to dinner.